Density Wave Theory of Spiral Arms

Image captured by the Atacama Large Millimeter/submillimeter Array (ALMA) features a protoplanetary disc surrounding the young star Elias 2-27, some 450 light years away. Image © B. Saxton (NRAO/AUI/NSF); ALMA (ESO/NAOJ/NRAO).
Earlier we have discussed two widely accepted theories of spiral arms; Gravitational Theory of the Origin of Spiral Structure of Galaxies and Magnetic Field Theory of Spiral Arms of Galaxy and now we are discussing even more widely accepted theory of spiral arms of disc galaxies; density wave theory of the spiral structure of spiral galaxy.
The density wave theory was first put forward by Chia-Chiao Lin and Frank H. Shu in the mid-1960s to explain the spiral arm structure of spiral galaxies, so also called Lin-Shu theory. Though several other scientists proposed and revised the previous density wave theories, this Lin-Shu density wave theory gave all authors the basic fundamentals.
In a series of papers (1964-1966), Lin and Shu first developed the basic logic and the mathematical formulation of problem of development of quasi-stationary, non-axisymmetrical, self-sustained, neutral, spiral density-waves as the manifestation of the gravitational instability in a thin material disc composed of stars and gas. One was published in 1964 in the Astrophysical Journal. Initially, astronomer thinks that the arms of spiral galaxy were materials but subsequently, that idea was reshaped. If the arms were materials then they become more and more tightly wound, since the matter nearer to the centre of the galaxy rotates faster than the matter at the edge of the galaxy. As a result, the arms would become indistinguishable from the rest of the galaxy after only a few orbits. This is called the winding problem.
Then later Lin and Shu proposed (in 1964) that the arms were not, in fact, materials as we thought but the arms itself are made up of areas of greater density.
More specifically, the density wave theory argues that the gravitational attraction between stars at different radii prevents the so-called winding problem, and actually maintains the spiral pattern. They develop the galaxy’s arms mode as similar to a traffic jam on our highway.
In a simpler example, they describe it as the cars move through the traffic jam: the density of cars increases in the middle of traffic jam itself, however, moves more slowly. Similarly, in the galaxy, stars, gas, dust, and other components move through the density waves, are compressed, and then move out of them.
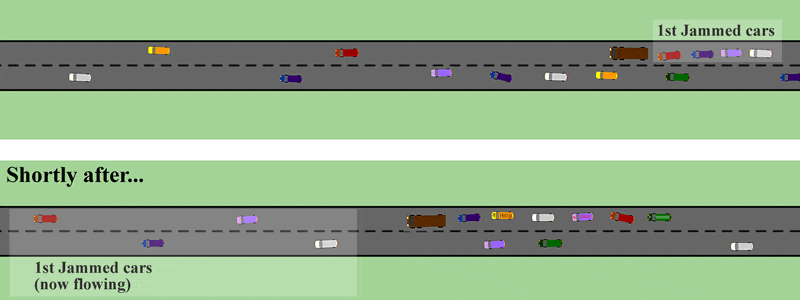
Here, the stars and interstellar material correspond to the cars that are moving much faster along the freeway than the truck and associated traffic jam (the high-density region of the spiral arm).
Subsequently, these authors and several others attempted in another series of papers to explain many of the observed dynamical and structural features in our galaxy in the light of density wave theory, thus exposing this theory to observational tests. Some of the features are random gas motion throughout the galactic disc, migration of stars away from the gaseous arms, large-scale MHD shock formation, first gaseous disc arm to be observed at a distance of 3 kpc from the centre, large thickness of the gaseous disc in the outer parts, etc.
The explanation of the star formation site on the spiral arms also lies in this theory; as time passes, the interstellar material moves into the region of high density and as above-defined our regular traffic jam model, those materials are compressed which in turn triggers star formation. These newly formed stars continue to orbit around the centre of the galaxy just like the interstellar matter from which they were formed.
Material condensation in the local regions of the galactic disc in the form of spiral arms appears to be a natural consequence of gravitational clumping and differential rotation in the disc. But as astronomer predicts that the differential rotation will also disrupt this local clumping in the long run, so the persistence of the formed spiral arms is more difficult to explain.
The density wave theory of Lin and Shu depends on the collective behaviour of the gravitational effects of stars and of gas. The analysis of Lin and Shu shows that the stars and gas in the galactic disc can maintain a spiral density-wave through gravitational instability in the presence of the differential rotation of the disc. The spiral density-wave gives rise to a spiral component of the gravitational field superimposed upon the general axisymmetric field. This spiral gravitational filed underlies the spiral arrangement of gas and young stars which can, in this way, be maintained over the entire scale of the disc.
The analysis of Lin and Shu show that non-axisymmetric disturbances of the spiral form can propagate around the galactic disc without being sheared to destruction even in the presence of differential rotation. This spiral pattern will therefore be stationary or at least quasi-stationary and thus the dilemma of winding and change of spacing is avoided. The simple theory is based on an assumption of zero-dispersion in velocities of gas and stars.
Further advancement of the density wave theory also let us explore other observations that are related to the spiral galaxies. Some are the ordering of H I clouds and dust bands, study the existence of young and massive stars, exploring the H II regions on the arms, and also the abundance of old, red stars in the remainder of the disk.
Now, we are discussing the mathematical explanation of the rotation of spiral arms. For this, we need to define a rotating coordinate frame - Ω0, which revolves at some speed. Similarly, for an axisymmetric disk with a flat rotation curve, the rotation speed Ω0 will coincide with the rotation speed at some radius Ω(R). Here, matters that were inside this radius, R, will appear to revolve in the direction of the frame rotation while those outside this corotation radius will revolve outside the direction if coordinate radius.
Now, a mass that completes two radial oscillations while performing one complete azimuthal trip in the rotating frame will give us elliptical orbits with the centre at the centre of the potential.
Azimuthal is an angular measurement in a spherical coordinate system which is an arc of the horizon measured between a fixed point (such as true north) and the vertical circle passing through the centre of an object usually in astronomy and navigation clockwise from the north point through 360 degrees.
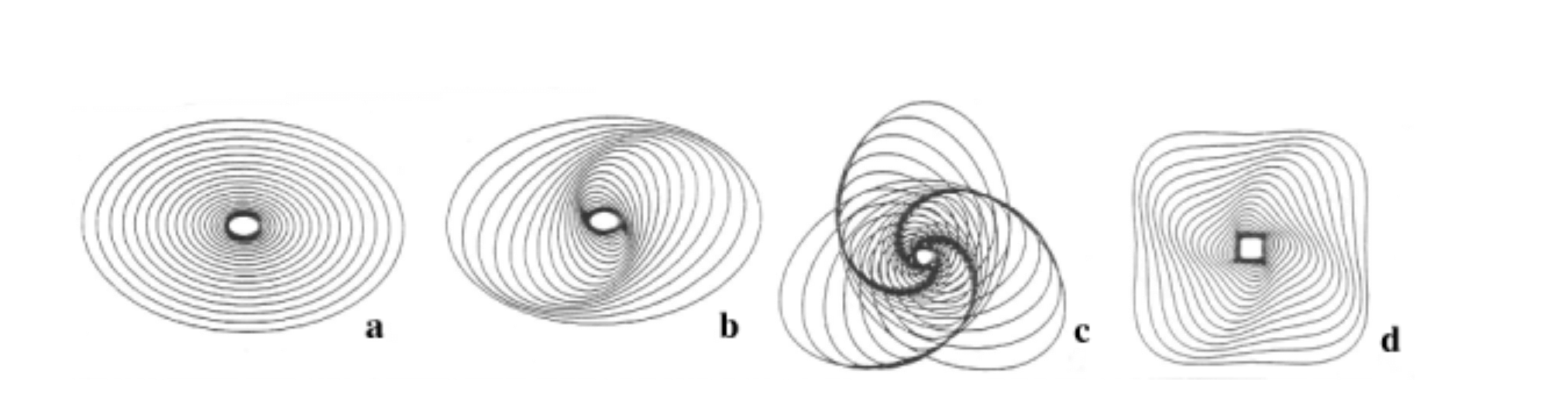
Similarly, a ratio of 3/2 gives a three-armed cloverleaf pattern. If we align a number of these 2/1 orbits concentrically and populate them with stars, the bar structure will be formed. This bar structure condition is particularly effective in the inner, rigidly rotating portions of a disk where the whole bar will rotate as a unit. Furthermore, by giving each successive concentric orbit a slight azimuthal offset, a spiral pattern can be formed. Clearly, when the majority of the stars are arranged in these spiral or bar patterns, the mass asymmetry will begin to affect the overall potential.
