Einstein Summation Convention, The Kronecker, and Levi-Civita Symbols

Einstein in 1916 developed the following notation scheme when manipulating expressions involving vectors, matrices, or tensors in general. 

The rules of summation convention are: 

1. Each index can appear at most twice in any term.

2. Repeated indices are implicitly summed over.

3. Each term must contain identical non-repeated indices.

For example:

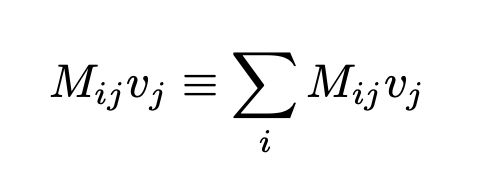
is a valid expression but

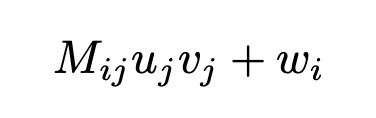
is not a valid expression in summation convention, since the index j appears three times in the first term.

Einstein summation implies the following;

For any vector quantity, V,

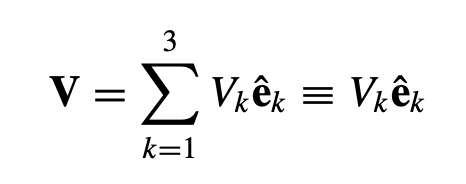
And the dot product of two vector quantity V and F is,

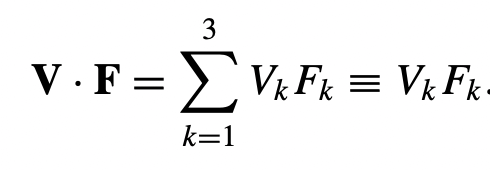
In a Cartesian basis, the gradient of a scalar (φ) and the divergence of a vector D can be variously written as,

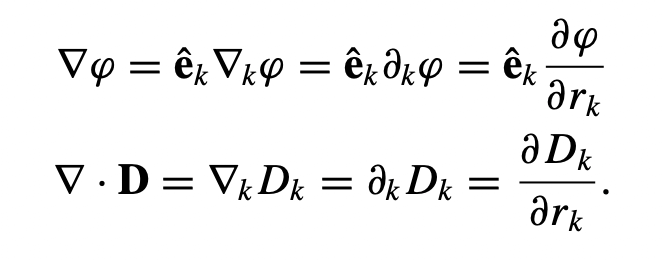
We can also easily get the matrix multiplication using the Einstein summation convection;

If an N × N matrix C is the product of an N × M matrix A and an M × N matrix B

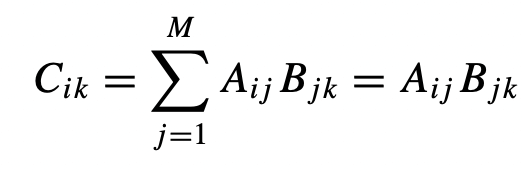
The Kronecker delta symbol δij is defined as,

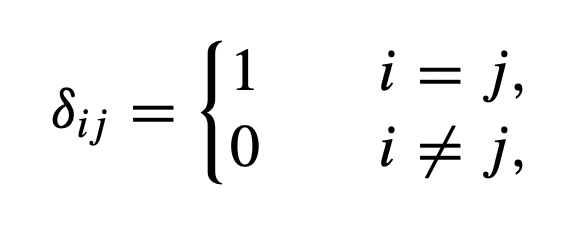
And Levi-Civita` permutation symbol ε_ijk is,

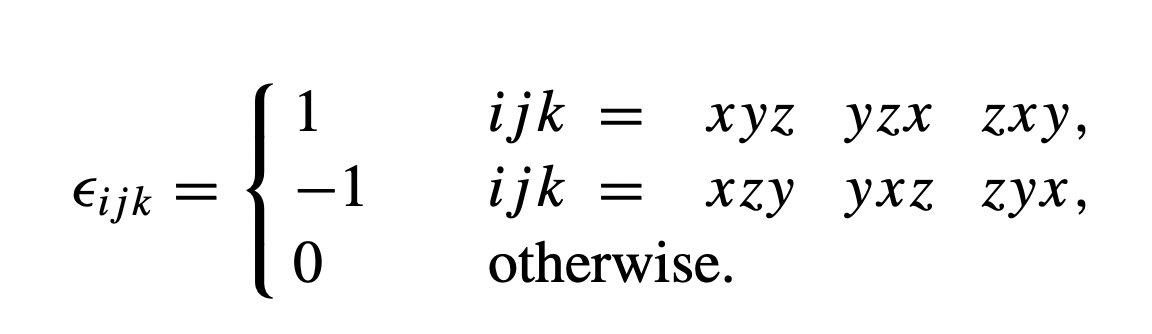
Notice that ‘1’ is for cyclic permutation of x, y, and z and ‘-1’ is for anti-cyclic permutation of x, y, and z. Zero is when, either i=j, j=k, or k=i.

That is, if we define x=1, y=2 and z=3 then Levi- Civita symbol holds following,

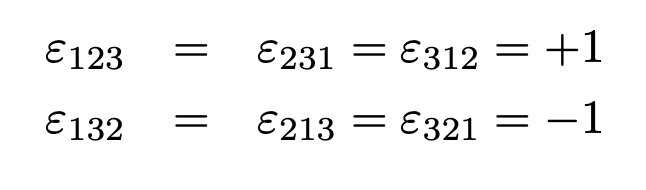
All other components are zero.

Using ε_ijk we can write index expressions for the cross product and curl. The ith component of the cross product is given by,

Now, [U✕V]₁ = 𝜺_1jkU_jV_k = 𝜺₁₂₃U₂V₃ + 𝜺₁₃₂U₃V₂ + all other terms zero

This gives [U✕V]₁ = U₂V₃ - U₃V₂

Similarly,

[U✕V]₂ = U₃V₁ - U₁V₃

And [U✕V]₃ = U₁V₂ - U₂V₁

Some other standard relations defined are,

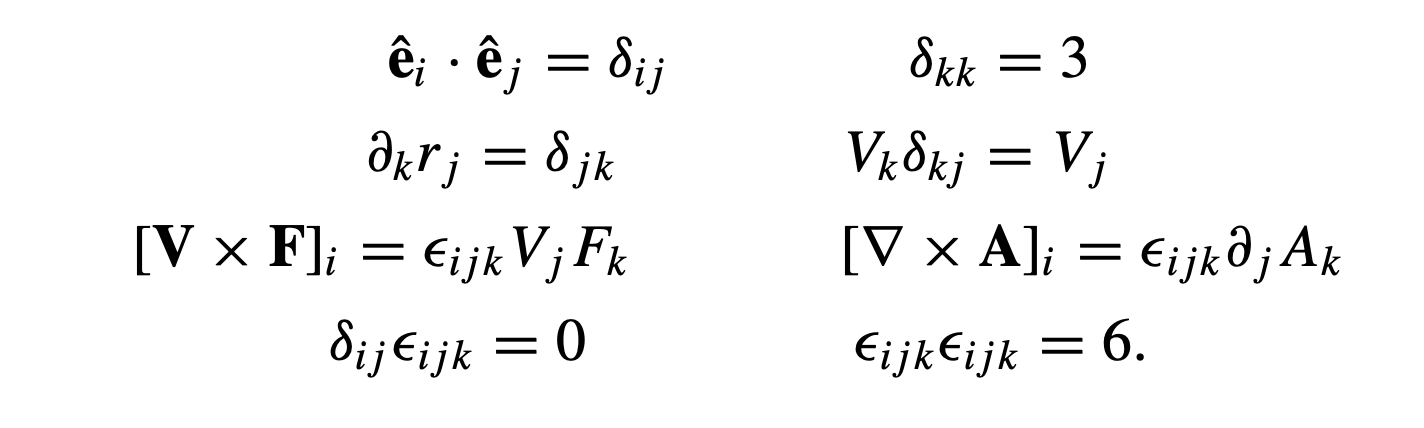
𝝏_kr_j means 𝝏_k/r_j 

Additionally,  𝜺_ijk𝜺_ist = 𝜹_js𝜹_kt - 𝜹_jt𝜹_ks 

𝜺_ijk = - 𝜺_jik

▽ = 𝝏_i and for any vector A, ▽A = 𝝏_iA_i.