Application of Gauss’s Law: Finding the Electric Field outside a Uniformly Charged Solid Sphere of Radius ‘R’ and Total Charge ‘q’

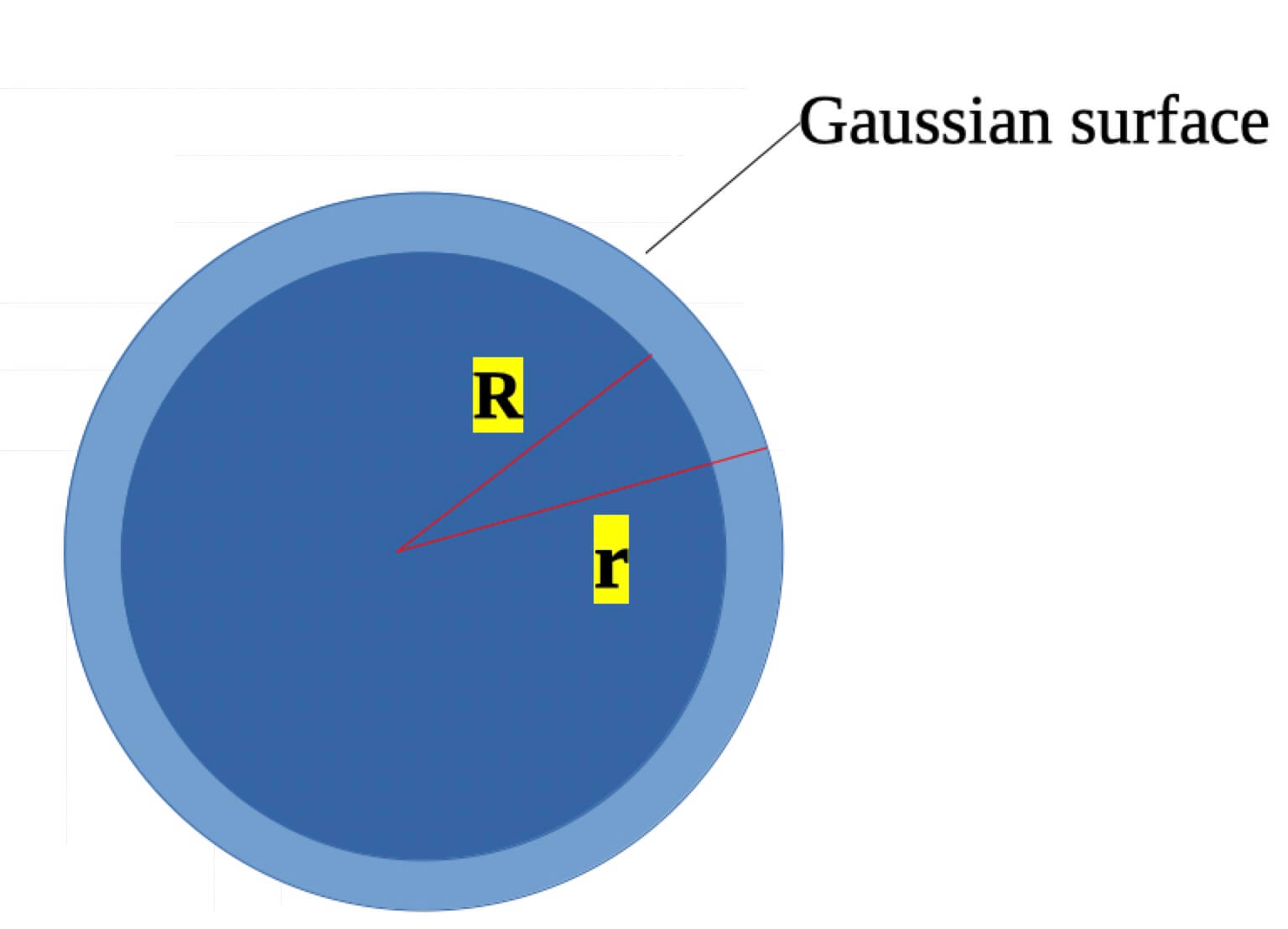
Figure 1.1. We are finding the electric field outside of the solid sphere (figure 1.1) whose radius is R.

To find the electric field using Gauss’s law, the first step is to draw a Gaussian surface where we are going to find the electric field. Since, in this problem, we are going to find the electric field outside of the sphere of radius ‘R’, we draw a Gaussian surface (in the form of the sphere) with radius, let’s say, ‘r’ (figure 1.2).

Gauss’s law says that for this surface (for Gaussian surface) the electric field 𝐸 through any closed surface S (a Gaussian surface) is equal to the net charge enclosed (Q_𝑒𝑛𝑐)divided by the permittivity of free space(𝜖₀):

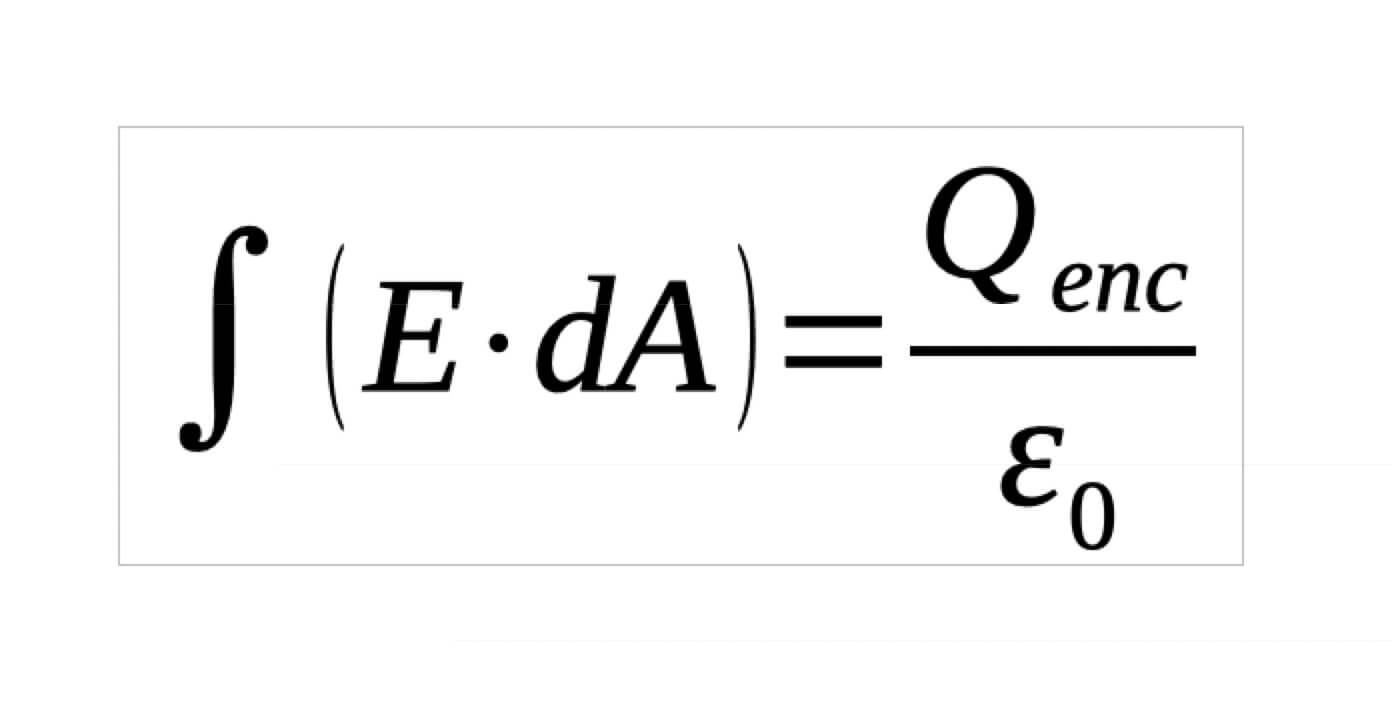
Where integration is over a closed surface (Gaussian surface). Q_enc is the total charge enclosed by the Gaussian surface.

Here as E points radially outward as does dA we can drop the dot product and the magnitude of E is constant over the Gaussian surface we can also take it out of the integral.

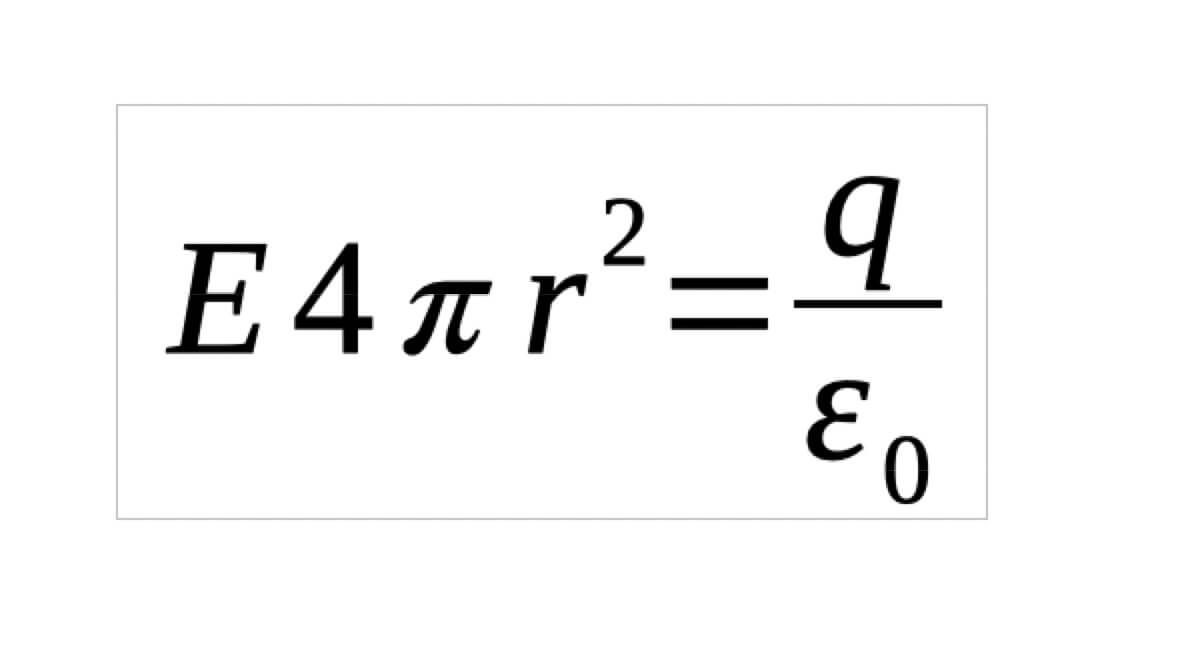
Here we have used the area of Gaussian surface (sphere) in place of dA we are given the total charge enclosed is q.

[I have directly used that dA inside the integration is the total surface area and the integration is over the Gaussian surface so it is the total surface area of the Gaussian sphere].

So, we get,

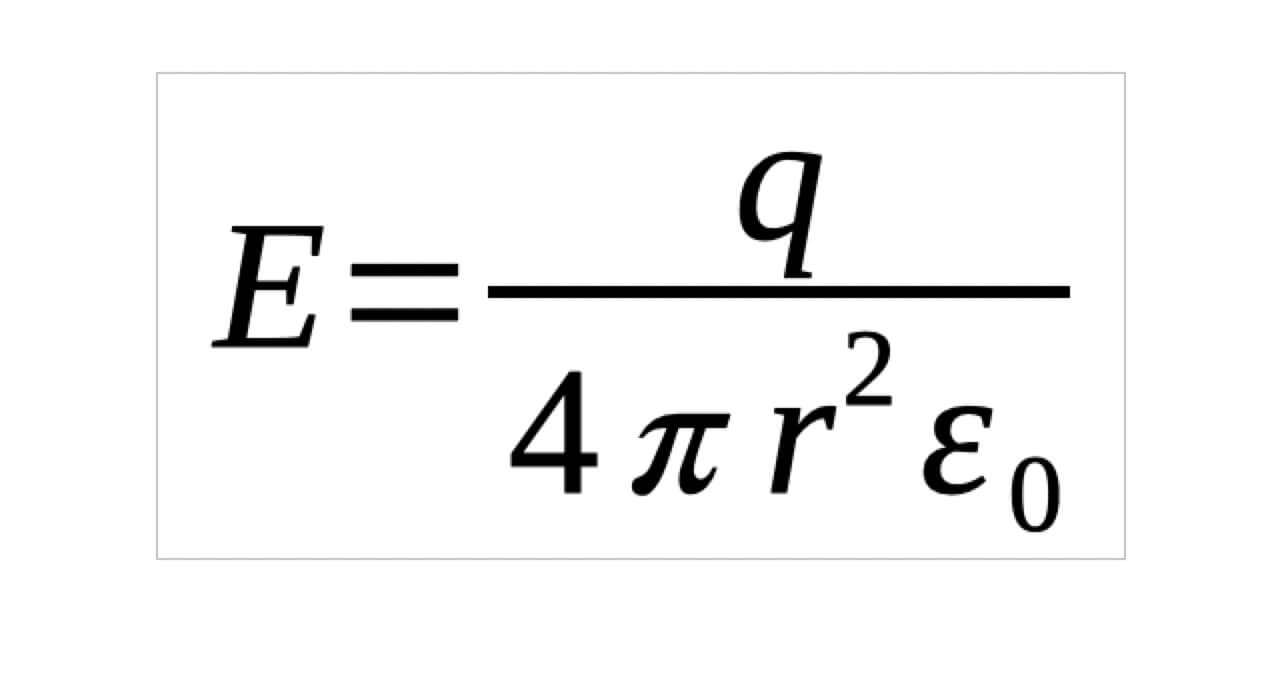
Tips for solving the problem using Gauss’s law:

For the following symmetry, it will be easier if we construct the Gaussian surface as follows;

1. Spherical symmetry: Make the Gaussian surface a concentric sphere.

2. Cylindrical symmetry: Make the Gaussian surface a coaxial cylinder.

3. Plane symmetry: Use a Gaussian ‘pillbox’ which straddles the surface.