How Do We Measure the Distance of Nearby Star From Earth?
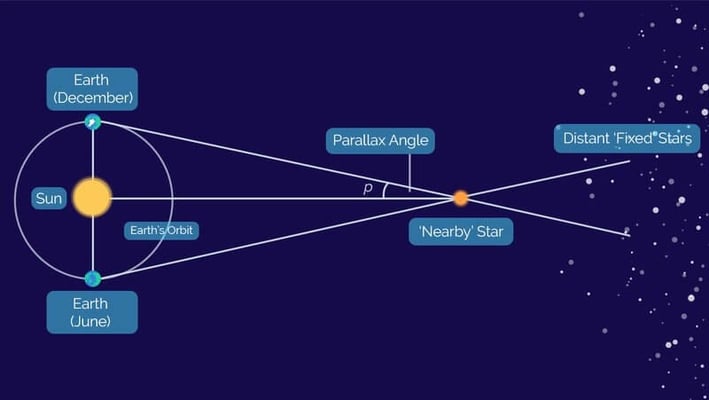
Image © Las Cumbres Observatory
Have you ever thought, wondered, and confused yourself on ‘how astronomers sitting here on Earth can estimate and claim the distance of the stars that are so much far away from us (even in many cases they are not visible from Earth), how they did this?’ For instance, the distance between the sun and the Earth is 151.53 million km and to measure this astronomer did not lay a measuring tape down to the sun from Earth. That is extremely impossible by the current technology we have and I think in the future too and the cost for this kind of space experiment is worthless too as we are able to observe the same things by using mathematics, trigonometry and some advanced designed equipment. So, how did they did this?
To predict the distance of the objects in space (mainly of stars so named stellar parallax), astronomers use a technique called the stellar parallax where they measure the apparent shift of position of any nearby star (or other objects) against the background of distant objects. As the name suggests; stellar- for the star and parallax- a displacement or difference in the apparent position of an object viewed along two different lines of sight.
Parallax is the change in viewpoint that occurs due to the change in motion of the observer, of the observed, or of both. There are different types of parallax according to its special field of use. Some are; stellar parallax, diurnal parallax, lunar parallax, solar parallax, moving-cluster parallax, dynamical parallax, and spatio-temporal parallax.
How Astronomers Measure the Parallax to Measure the Distance of Star?
Stellar parallax was first measured by Friedrich Bessel of Germany in 1838 for the star 61 Cygni. Bessel measured its distance to be 10.4 light-years which very close to the actual value of about 11.4 light-years. Similarly, Thomas Henderson first measured the parallax of 𝝰 Centauri and found the value to be 0.75″, which means the distance 1/0.75, or 1.333 parsecs which is equal to 4.347 light-years. The nearest star to the Earth, Proxima Centauri has the measured parallax of 0.76813″, which means 1/ 0.76813 parsec 4.24 light-years away from the Earth.
Now Here is How We Measure the Parallax of the Star?
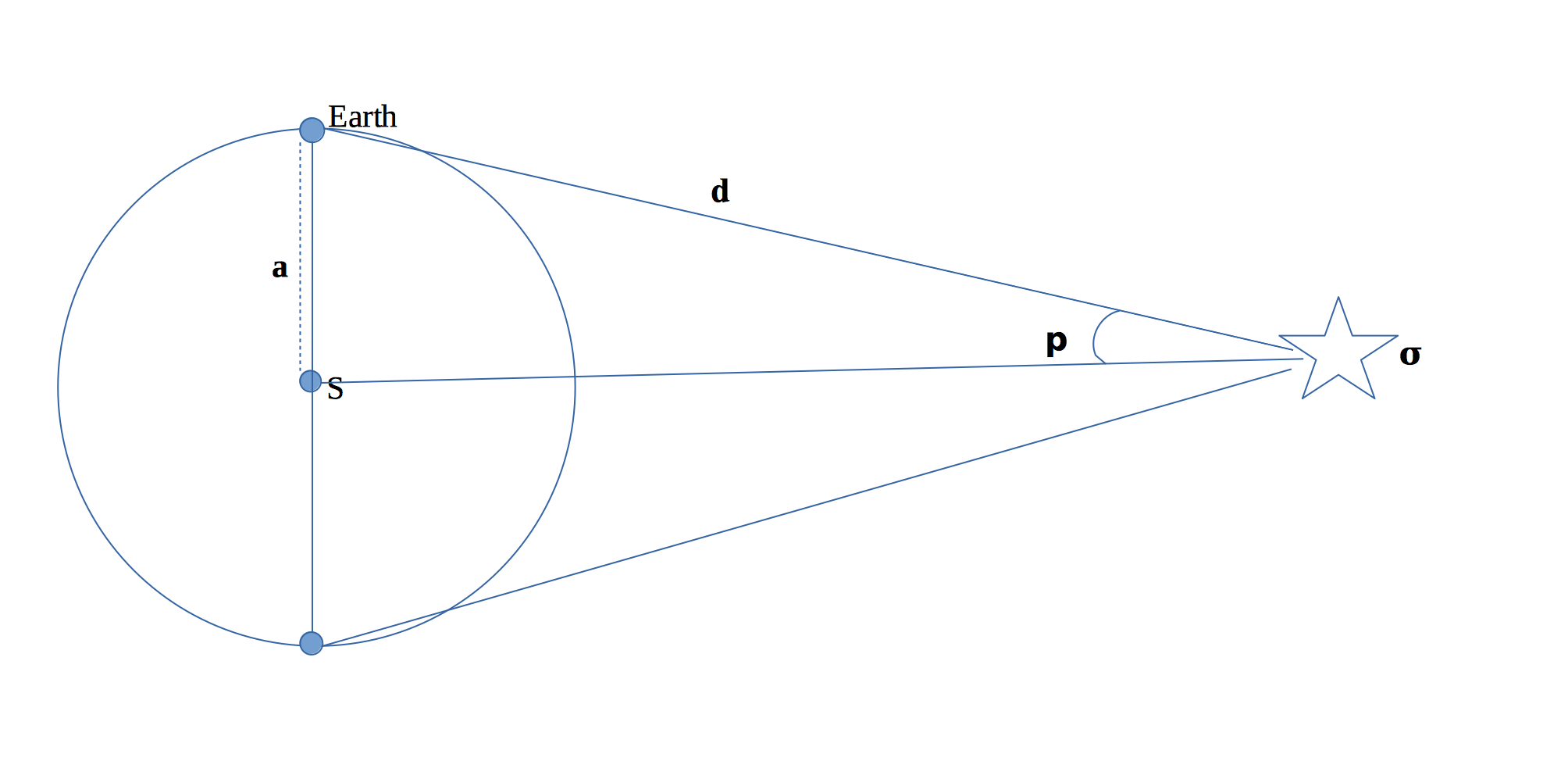
To measure the parallax of a nearby star, a widely used method is trigonometric parallax where the diameter of the Earth’s orbit around the sun is used as a basic line of measurement. Thus the trigonometric parallax of a star may be defined as the angle ‘p’ (in second or arc) subtended at the star ‘𝛔’ by the mean radius ‘a’ of the Earth’s orbit around the sun. This is also called a heliocentric or annual parallax.
Related: Stellar Magnitude
For this, the position of a nearby star is measured from two points of Earth, on the opposite sides in six months apart. Doing this, relative to a background of very remote, fixed star, astronomers will observe a small angular displacement.
A nearby star '𝛔’ is photographed from the position E of the Earth against the background of the far off stars. Similar observations are also made from the opposite position E', after six Earth months. From these observations, the angle subtended by the diameter EE' (or the baseline) at the star ‘𝛔’ is measured by comparing the change in the position of ‘𝛔’ during those six Earth month period with respect to the fainter far off stars whose shift in position due to the motion of the Earth is negligible. Now the one half of this angle gives the measure of annual parallax '𝗽' of the star. The sets of observations at E and E' are repeated when the Earth comes back to this position after a year and the average of a number of measurements will be taken as the parallax '𝗽' of the star.
As the stars are too far away, the parallax of a star is a very small angle and its value has been found to be always less than 1″ of arc even for the nearest stars.
Prad = a/d where a is the baseline length and d seems to be a hypotenuse length between the star '𝛔' and the point of observation of Earth but in fact, is the distance between the Earth and the star. (Don’t be confused and self assume, seeing the above figure, that the center is the Earth and the distance d is the hypotenuse length between the Earth and the star).
Then 1rad = 206,265″ of arc.
We may get, finally, d = 1/𝗽″
Where d is in parsec (pc). When 𝗽 = 1 then d = 1 which is the definition of parsec; a parsec is a distance at which the radius of the Earth’s orbit (1 AU) subtends an angle of one second of arc. [1 pc ~ 3.26156 light-years ~ 63241.1 AU]
In terms of light-years, this will changes into,
d = 3.26/𝗽″
Remember that this distance d is not the hypotenuse length between the star and the point of view but the distance between the star and the Earth.
Though used in most cases, it is not an absolute technique. Parallax angles less than 0.1 arcsec are very hard to measure by this method as by the effect of Earth’s atmosphere which in turn limits the Earth’s ground-based telescopes in measuring the distances to stars about 1/0.01 or 100 parsecs away. However, space-based telescopes can have accuracy up to 0.001 parsecs. So, this method is not fit for all methods.
Another trick to measure the distance in space is bouncing a laser light method. For instance, astronauts in 1969 walked on the moon and left reflectors behind. Those reflectors are being used to bounce the laser light from Earth and using the speed of light and the time it takes for the laser beam to return to Earth, astronomers measure the precise distance between the moon and Earth.

Other Lunar reflectors are also placed by the United States and also by the Soviet Union, altogether five reflecting panels.
