Johannes Kepler in between 1609 and 1619 (first two laws in the year 1609 and a third law in 1619) modified the earlier concept of the heliocentric theory of Nicolaus Copernicus - replacing its circular orbits and epicycles with elliptical trajectories, and explaining how planetary velocities vary, published three laws that describe how planetary bodies orbit about the Sun.
The usefulness of Kepler’s laws extends to the motions of natural and artificial satellites, as well as to stellar systems and extrasolar planets.
They describe how planets move in elliptical orbits with the Sun as a focus, a planet covers the same area of space in the same amount of time no matter where it is in its orbit, and a planet’s orbital period is proportional to the size of its orbit (its semi-major axis).
Being fundamentally laid on Newton’s work and laws, these laws laid the basic foundation for the motion of planetary motion and still valid law in astronomy.
Kepler's First Law (The Law of Ellipses)
Planetary orbits are elliptical with the sun at a focus.
Each planet orbit about the Sun is an elliptical orbit and the host star always located at one focus of the orbital ellipse. For instance, the sun; the sun lies the centre of our solar system and the path followed by the planets including the Earth is elliptical, in real.
The first law also signifies that the planet to Sun distance is constantly changing as the planet goes around its orbit (in an elliptical orbit).
Kepler's Second Law (The Law of Equal Areas)
A line joining a planet and the Sun (radius vector) sweeps equal areas in equal times.
As the planet revolves around the host star in an elliptical path, their speed varies; a planet moves fastest when it is closest to the sun and slowest when it is furthest from the sun, yet the line joining the centres of the Sun and the planet sweeps out equal parts of an area in equal times.
Therefore the ellipse traced by a planet around the Sun has a symmetric shape, but the motion is not symmetric.
For instance, if an imaginary line were drawn from the earth to the sun, then the area swept out by the line in every 31-day month would be the same.
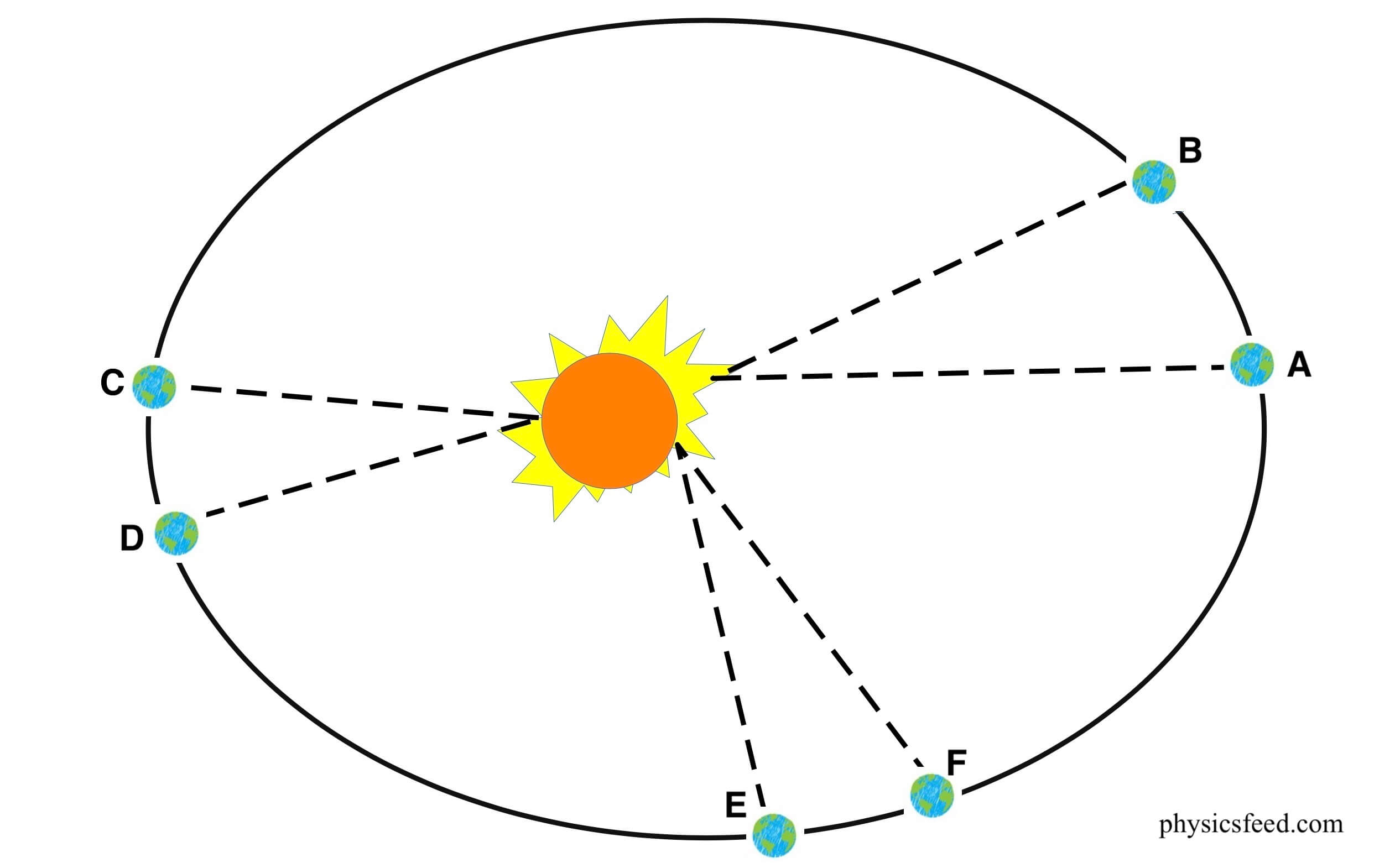
As can be observed in the diagram, the areas formed when the earth is closest to the sun can be approximated as a wide but short triangle; whereas the areas formed when the earth is farthest from the sun can be approximated as a narrow but long triangle.
Since the base of these triangles is shortest when the earth is farthest from the sun, these areas are the same size and the earth would have to be moving more slowly in order for this imaginary area to be the same size as when the earth is closest to the sun.
Kepler's Third Law (The Law of Harmonies)
The ratio of the square of the period of revolution and the cube of the ellipse semimajor axis is the same for all planets.
Kepler’s third law of planetary motion compares the orbital period and radius of orbit of a planet to those of other planets and provides an accurate description of the period and distance for a planet's orbits about the sun.
Kepler discovered that the size of a planet's orbit (the semi-major axis of the ellipse) is simply related to the sidereal period of the orbit. If the size of the orbit (a) is expressed in astronomical units (1 AU equals the average distance between the Earth and the Sun) and the period (P) is measured in years, then Kepler's Third Law says:
P2 ∝ a3
After applying Newton's Laws of Motion and Newton's Law of Gravity we find that Kepler's Third Law takes a more general form:
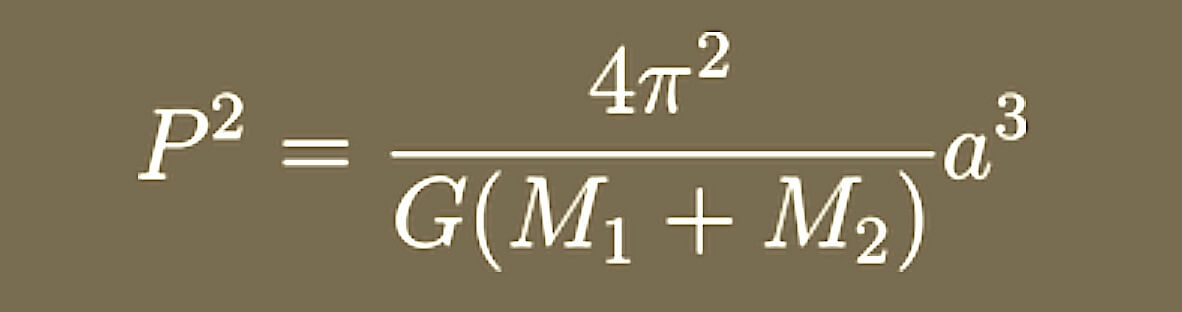
where M1 and M2 are the masses of the two orbiting objects in solar masses. Note that if the mass of one body, such as M1, is much larger than the other, then M1+M2 is nearly equal to M1. In our solar system M1 =1 solar mass.