Image © NASA/SDO/AIA
The light particles (photons) generated at the Sun’s centre take almost 10 million years to radiate into space and additional 8 minutes and 20 seconds to reach the Earth.
Stars like Sun generates energy (light, heat) by a process called nuclear fusion where two or more atomic nuclei are combined to form one or more different atomic nuclei and subatomic particles and the difference in mass between the reactants and products is released as energy. During this whole process, a capable star (depend on how massive the star is) can produce higher elements, typically up to iron and gold.
The time taken by a photon (to travel from the centre of star to the surface) and the path is governed by a theory called the theory of random walk and describes the path of a photon from the centre of a star to its surface.
Theory of random walk describes this enormously time taking process as the consequences of repeatedly absorbing and reemitting the photon and also in a random direction.
Here is how the theory of random walk predicts the time taken by a photon from the centre of its star to reach the surface.
Let the step length of the walk (the mean free path) be d. Consider, for simplicity, the random walk in a plane. After one step the photon is absorbed in distance,
x1 = d cos𝜃1,
y1 = d sin𝜃1
Where 𝜃1 is an angle giving the direction of the step.
Now the position coordinate after N steps is given by the summation of all the steps; from i = 1 to i = N
x = ∑ d cos𝜃i ,
y = ∑ d sin𝜃i
Then the distance from the starting point is
r2 = x2 + y2
= d2 [(∑cos𝜃i)2 +(∑sin𝜃j)2] the summation is from 1 to N.
Now the first term in the above square bracket,
(∑cos𝜃i)2 = (cos𝜃1 + cos𝜃2 + cos𝜃3 + ..... + cos𝜃N)2
Since the directions, θi are randomly distributed and independent, we can use
For i ≠ j, ∑cos𝜃i cos𝜃j = 0
And the same rule also applies for the second term of the above square bracket.
Finally, we can get
r2 = d2 ∑(cos𝜃i2 + cos𝜃j2), the summation is from i = 1 to i = N
Hence, r2 = Nd2
So, r = d √N
This value of r is the distance of photon from the starting point after N steps.
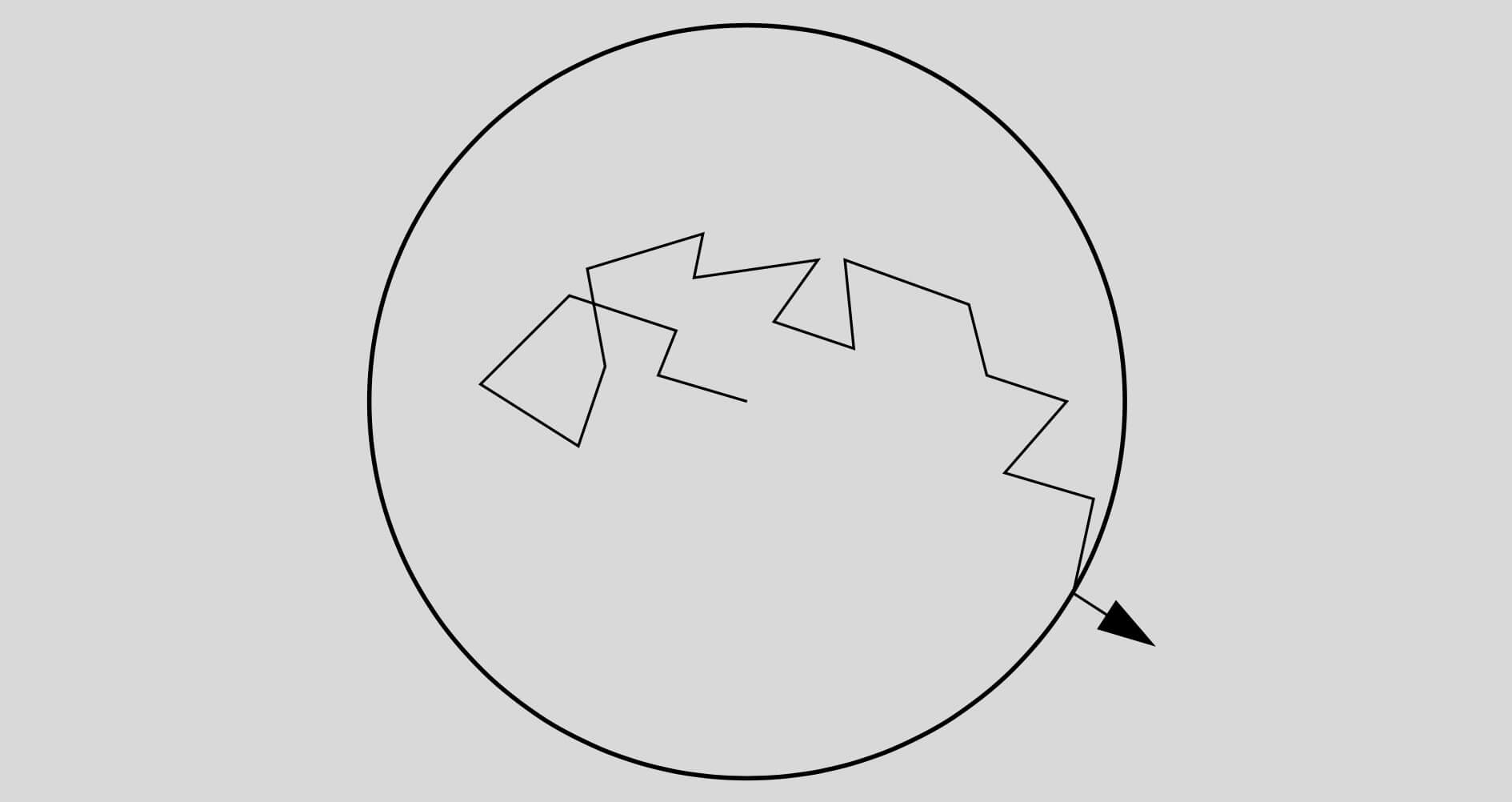
This process is similar to a drunkard taking a hundred one-metre steps at random and wandered just ten metres from his/her starting point.
From the calculation, we can get the mean free path of the photon as 10-4 m and this value is a reasonable estimate in most of the solar interior.
Since the solar radius r = 109 m, the number of steps needed to reach the surface will be N = (r/d)2 = 1026. The total path travelled by the photon is given by s = Nd = 1022 m, and the time taken is t = (s/c) = 106 years; a more careful calculation gives t = 107 years.
Thus it takes 10 million years for the energy generated at the centre to radiate into space.