To describe any physical quantity like velocity and acceleration that mostly describe the nature of path of particle in space we need to assign a coordinate system depending on geometry, depending on the type of problem under consideration, and symmetry of the object.
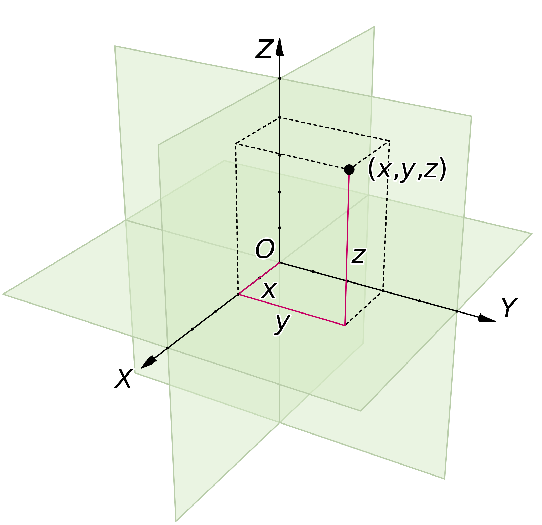
Rectangular coordinate system is the simplest coordinate system that consists of coordinate axes oriented perpendicularly to each other and we generally call them X, Y, and Z-axe, in three dimension.
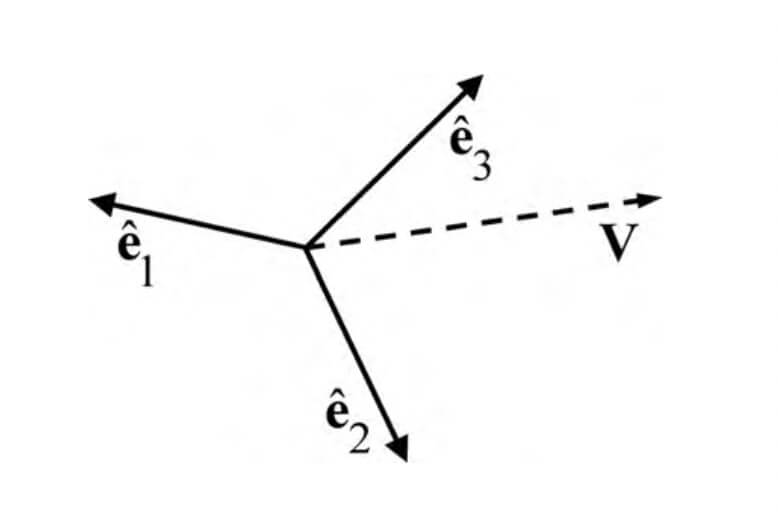
The notation for cartesian components and unit vectors is
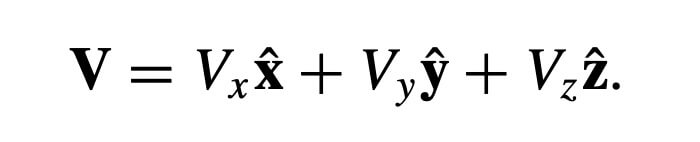
And the position vector is
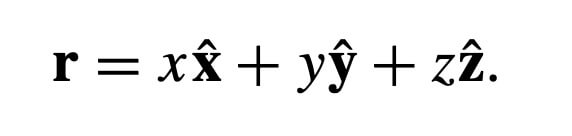
Where,

is the unit vector along X- axis. This basically define the direction along the particular axis. Similar is for Y and Z- axes.
If we can find the position vector r of particle then we can define quantities like velocity (which is derivative of position) and acceleration (which is derivative of velocity).
Gradient operator in cartesian representation is
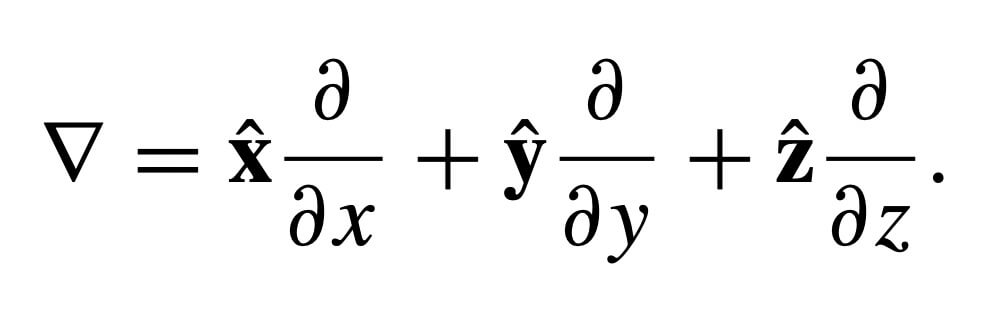
Divergence is;
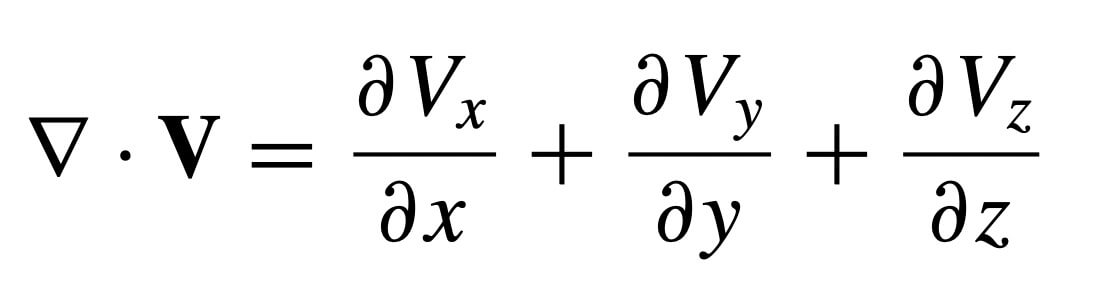
Curl is;
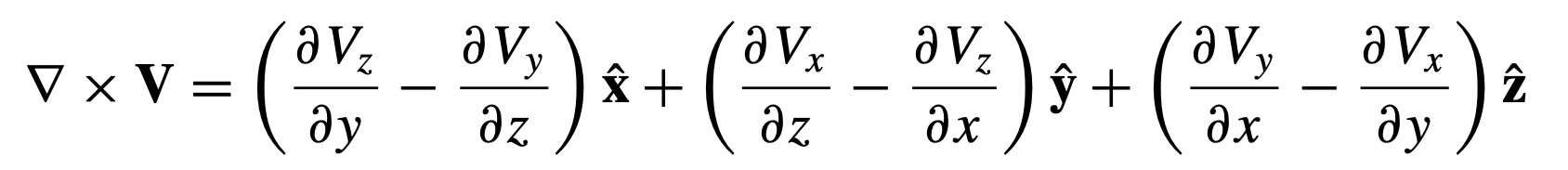
And laplacian is;
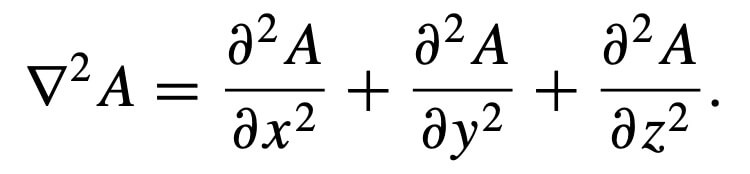
The divergence and curl are more easily given by using Einstein Summation Convention.
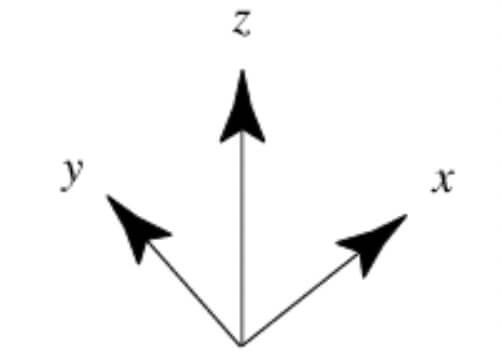
There are two types of cartesian coordinate systems called right-handed coordinate system and left-handed cartesian coordinate system. In three dimensions, so-called right-handed coordinate systems (left figure) are usually chosen by convention.
For right-handed coordinates the right thumb points along the z axis in the positive direction and the curl of the fingers represents a motion from the first or x axis to the second or y axis.
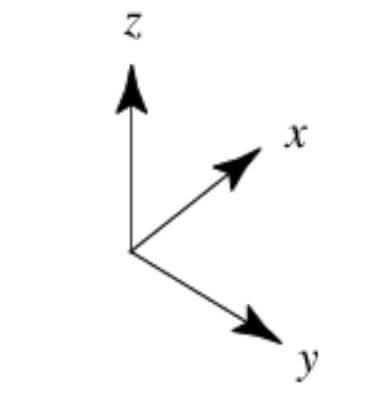
In right-handed coordinate system the positive x and y axes point right and up, and the negative z axis points forward whereas in left-handed coordinate system the positive x, y and z axes point right, up and forward, respectively.