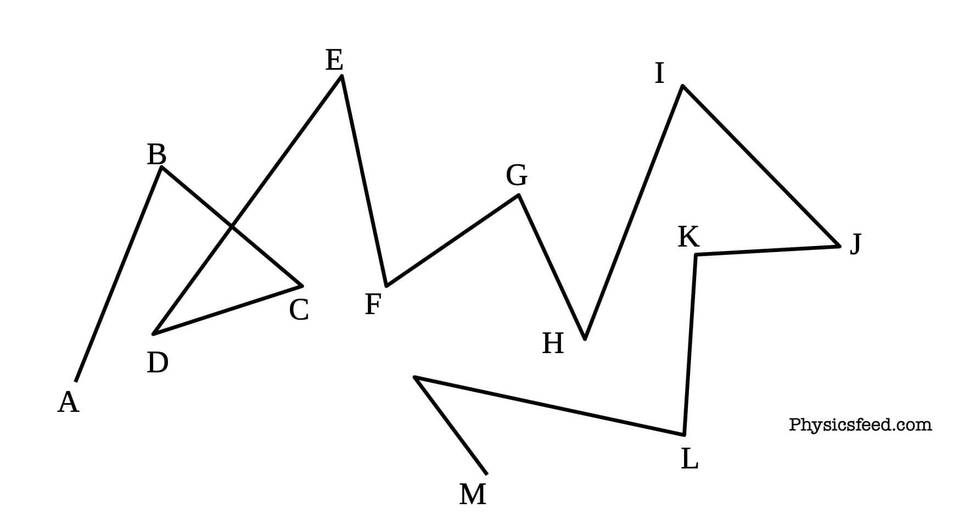
We will be concerned to obtain the probability of finding a randomly moving particle at a particular point on its track.
Let a drunk starts from point A and walk randomly at positions following B, C... to point M as shown in the above figure.
Let’s first generalize the problem. Let us consider that drunk man who starts out from a lamppost located on a street. Each step he takes is of equal length l. The man is however so drunk that the direction of each step, whether it is to the left or right, is completely independent of the preceding step. Let the probability that man taking steps towards the right side is p and to the left is q where q = 1 - p.
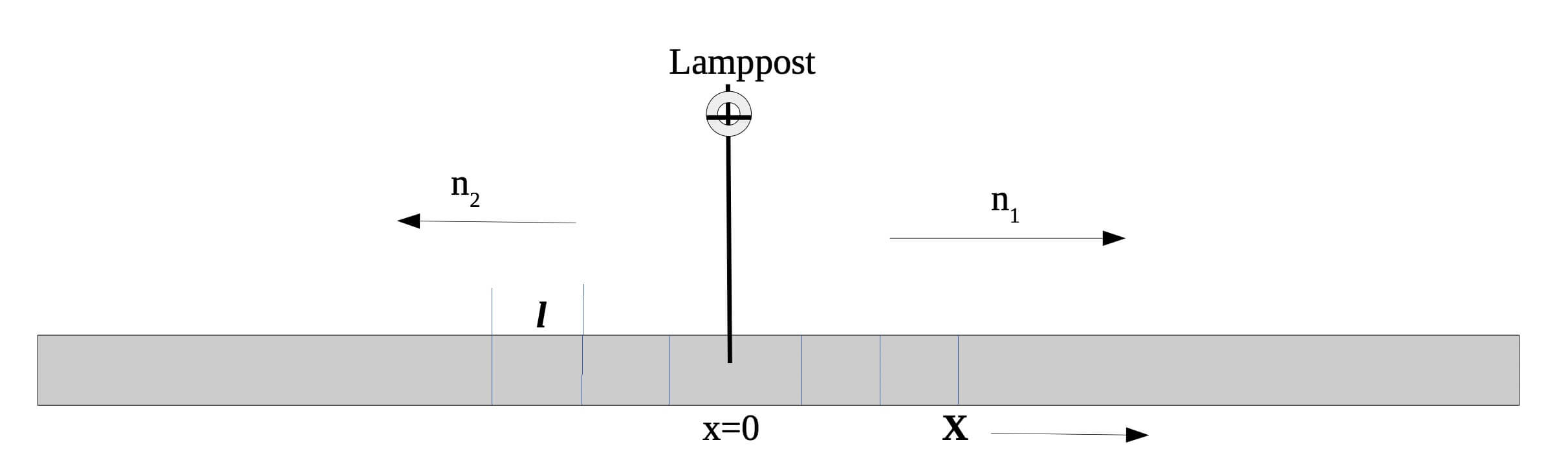
We are interested to find the probability of that man being located at position x=ml.
Since each step is of length l, the location of the man along the x-axis must be of the form x=ml where m is an integer (can be positive, negative, or zero).
In general, this problem illustrates the one adding N vectors of equal length but then asking for the probability that their resultant vector sum has a certain magnitude and direction.
Now instead of talking in terms of drunk taking steps, let us revert to the less alcoholic vocabulary of physics and think of a particle performing successive steps or displacements in one dimension.
After N steps each of length l, the particle is located at
x = ml
Where m is an integer in between -N to N i.e -N ≤ m ≤ N.
Now we want to calculate the probability P(m) of finding the particles ate the position x = ml after N steps.
While the particle is making steps, it can take steps to the right or left. So, let us denote the number of steps to the right by n1 and to the left by n2. Then
N = n1 + n2 ------------(1)
The net displacement measured to the right in units of a step length is m = n1 - n2
This yield
m= n1 - (N-n1) = 2n1 - N ------------------(2)
This equation shows that if N is even m becomes even and if N is odd then m also becomes odd regardless of the value of n1 since the 2n1 becomes automatically even if n1 is odd.
Irrespective of the past history, each step is characterized by the respective probability denoted by
p = probability that the particle step is to the right
q = 1 - p = probability that the particle step to the left.
Now, since the particle may step n1 steps to the right and n2 steps to the left with respective probabilities p and q, the probability is given by the product of p and q for n1 and n2 times i.e.
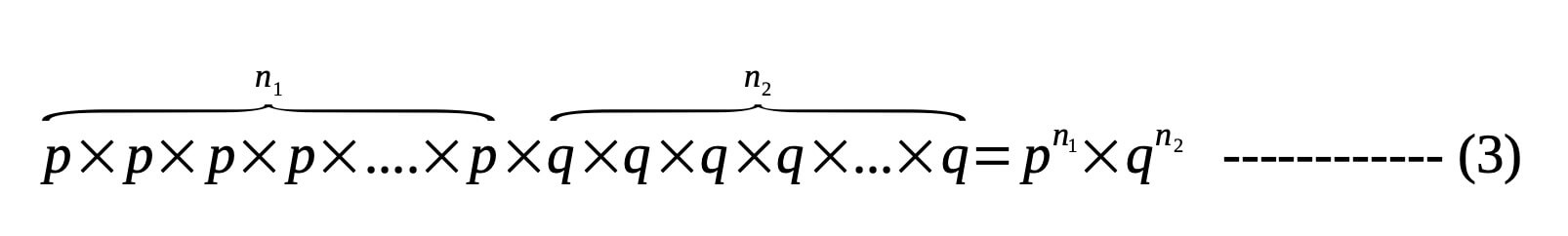
But there exist many different possible ways of taking N steps so that n1 of them are to the right and n2 are to the left. So the number of distinct possible ways, among N steps, we can arrange n1 steps to the right and n2 steps to the left are given by

Hence the probability W(n1) of taking n1 steps to the right and n2 steps to the left in any order is given by multiplication of probability in equation (3) and expression of equation (4).
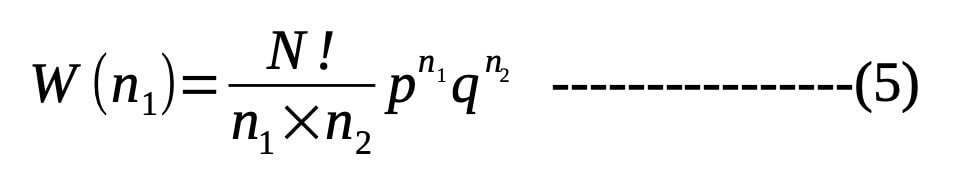
The above probability equation is called the binomial distribution. This equation represents a typical term encountered in expanding (p+q)N i.e.
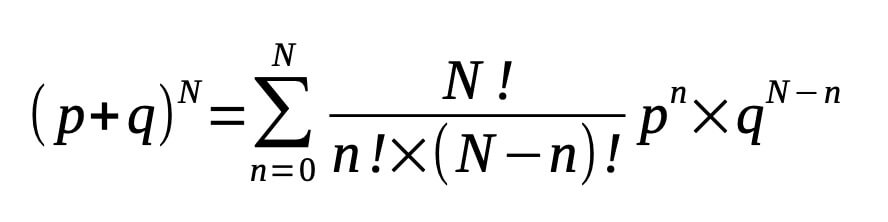
If it is known that the particle has performed n1 steps to the right in a total of N steps, then its displacement from the origin can be determined. This is shown by equation (2).
Thus the probability P(m) that the particle is found at position m after N steps is the same as W(n1), i.e. P(m) = W(n1).
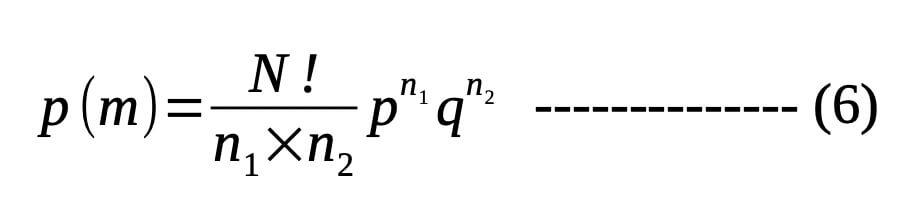
This p(m) is used in statistical mechanics to deal with the probability of a very large number of particles ranging to Avogadro’s number of particles and also the spin system; however, other standard calculations are required.