Stellar Magnitude
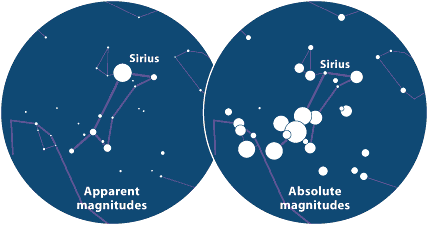
On the left-hand map of Canis Major, dot sizes indicate stars' apparent magnitudes; the dots match the brightnesses of the stars as we see them. The right-hand version indicates the same stars' absolute magnitudes - how bright they would appear if they were all placed at the same distance (32.6 light-years) from Earth. Absolute magnitude is a measure of true stellar luminosity.
Stellar magnitude is a way to measure the brightness of stars. Though the brightness of the star varies depending on its chemical composition and its distance from the observer, measuring the exact brightness that will be the same for all the observer is an important aspect in the field of astronomy.
Stellar magnitude is a measure of the brightness of a star or other celestial body.
To actually measure the brightness of the distant stars and to make the brightness of star a universal and uniform, astronomers came out with a new technique of measurement called the absolute magnitude.
Brief History
About 2,000 years ago, a great Greek astronomer- Hipparchus, first introduced the concept of magnitude of brightness of a star. He is believed to the first astronomer who successfully made the well-known catalogue of stars according to their brightness. Hipparchus ranked his stars in a simple way; he gave numbers (magnitude) to the star according to their brightness; he called the brightest ones "of the first magnitude," simply meaning "the biggest." Stars not so bright he called "of the second magnitude," or second-biggest. The faintest stars he could see he called "of the sixth magnitude."
Later as the astronomers went on exploring the vast universe with the new tools and telescope, they saw a pressing need to define the entire scale of the stellar magnitude system more precisely than by eyeball judgment. Though Galileo was the first to start thinking about the change in the magnitude system of the brightness of stars, many other astronomers like Ptolemy also added in this journey. Consequently, as the telescope becomes more and more sophisticated astronomers kept adding more magnitudes to the bottom of the scale. For instance, today a pair of 50-millimeter binoculars will show stars of about 9th magnitude, a 6-inch amateur telescope will reach to 13th magnitude, and the Hubble Space Telescope has seen objects as faint as 31st magnitude.
The stellar magnitude scale works 'in reverse': objects with a negative magnitude being brighter than those with a positive magnitude. Hence the more negative the value, the brighter the object is.
Accordingly, astronomers determined that a 1st-magnitude star shines with about 100 times the light of a 6th-magnitude star. So, in 1856 the Oxford astronomer Norman R. Pogson proposed that a difference of five magnitudes be exactly defined as a brightness ratio of 100 to 1. One magnitude thus corresponds to a brightness difference of exactly the fifth root of 100 ( 5√100), or very close to 2.512. This value is known as the Pogson ratio. Consequently, a magnitude 1 star is about 2.5 times brighter than a magnitude 2 star, (2.5)2 brighter than a magnitude 3 star, (2.5)3 brighter than a magnitude 4 star, and so on. This convenient rule was quickly adopted.
Mathematically, if Bm and Bn (n>m) be the brightness of two stars having magnitudes m and n respectively, then Bm ➗ Bn = 100.4 (n-m)
The above equation also shows- higher the magnitude of a star, lower is its brightness and vice-versa.
Problem with the older version of magnitude measurement
By the late 19th century astronomers started using photography to record the sky and measure star brightnesses. But a problem popped up: some stars showing the same brightness to the eye showed different brightnesses on film and vice versa.
Similarly, different photographic emulsions have different spectral responses and the difference in the colour sensitivity of the observer’s eye also assists in the real magnitude problem. For instance, as human turns old, their eye lenses turn yellow and they see the world through yellow filters. The magnitude systems designed for different wavelength ranges had to be more clearly defined than this.
Just seeing through telescopes is not enough. And here is the adopted solution.
Astronomers exploit the fact that compared to the human eye, photographic emulsions were more sensitive to blue light and less to a red light. Accordingly, two separate scales called the visual magnitude (mvis) and photographic magnitude (mpg) were devised where (mvis) describes how a star looked to the eye and (mpg)/(mp) referred to star images on blue-sensitive black-and-white film. The difference in the value of mvis and mpg is called the colour index.
Stellar colour index is the numerical value that determines the colour of an object, which ultimately gives the temperature of the star. The rule is simple; the smaller the colour index, the more blue (or hotter) the object is, and larger the colour index, the more red (or cooler) the object is.
Depending on this, nowadays astronomers use a standard photoelectric photometer what gives us a precise magnitude. Among many photometric systems, one most common and exact is UBV photometry (U stand for near-ultraviolet, B for blue, and V for visual magnitude). This photometry wide peak lies in the yellow-green band, where the eye is most sensitive.
So, now the colour index is known and calculated as B minus V (mathematically, B-V). A pure white star has a B-V of about 0.2, our yellow Sun is 0.63, orange-red Betelgeuse is 1.85, and the bluest star believed possible is -0.4, pale blue-white.
Later to cover all the wavelengths UBV system was extended towards the red end of the spectrum with R and I filters to define standard red and near-infrared magnitudes. Hence it is sometimes called UBVRI. On the successive extensions, it was finally able to carry still longer wavelengths, picking up alphabetically after I to define the J, K, L, M, N, and Q bands.
Here, for all the wavebands, the bright star Vega has been chosen (arbitrarily) to define magnitude 0.0. i.e. the reference star for the scale.
Apparent magnitude Vs. absolute magnitude
In practical observation, there are two main types of magnitudes. One is the apparent magnitude, and another is the absolute magnitude.
Apparent magnitude (denoted by m) is the magnitude of the star that appears to the observer at Earth wherever be the star is and this value of magnitude depends on the location of an observer. This means for the same star looking from a different location at Earth, the magnitude varies, and the star that is closer to Earth, but fainter, could appear brighter than far more luminous ones that are far away and this, which obviously create a discrepancy in the observation.
So, we need to establish a convention whereby we can compare stars on the same footing, without variations in brightness due to differing distances. So astronomers formulated a technique known as absolute magnitude (intrinsic/true magnitude).
Stellar absolute magnitude is usually denoted by M with a subscript to indicate the passband. For instance, MB is the magnitude of the star at 10 parsecs in the B passband.
Absolute magnitude is the brightness of stars as they would appear if it were at 10 parsecs or 32.6 light-years away from Earth. This measurement of stars at a particular fixed distance (10 parsecs) from earth solves the problem of varied brightness measurement of star and the measurement actually depends on the intrinsic brightness of star rather than its distance.
Mathematically stellar absolute magnitude is given by
m - M = 5 log d - 5
where m is the apparent stellar magnitude, M is the stellar absolute magnitude, and d is the distance measured in parsec.
[1 parsec ~ 3.26 ligh-year]
The quantity (m-M) is called distance modulus and it utterly depends on the value of d.
Two kinds of distance moduli are (m-M)v is the visual distance moduli and (m-M)o is the true distance moduli.
Some astronomical terms that are linked with the stellar magnitude
Luminosity: Generally, luminosity is understood as the level of brightness but in reality, it is not that simple, however, technically linked with. Luminosity is an absolute measure of radiated electromagnetic power or light. This means the measure of the radiant power emitted by a light-emitting object.
In astronomy, luminosity is also the measure of the total amount of electromagnetic energy emitted by a star, galaxy, or any other astronomical object but per unit time. This also defines luminosity as the total power (electromagnetic energy per unit time) emitted by a star.
In general, luminosity is measured in joules per second, or watts but in astronomy, values for luminosity are often given in the terms of the luminosity of the Sun (L⊙).
Bolometric magnitudes:
All the stellar magnitudes defined so far only cover some limited regions of the stellar spectrum but the spectrum in the reality of wide and to understand the universe and its creation we have to study those missing spectrum. So to cover all the spectrum range of the radiated electromagnetic radiation, not just the portion visible as light, astronomers defined a magnitude called bolometric magnitude (mbol). Bolometric magnitude is the measure of the total radiations emitted by a star at all wavelengths.
Though some of the wavelengths of the electromagnetic radiation from the stars are blocked either partially or completely by the Earth’s atmosphere, modern observations provide measurements of the star’s spectrum from orbiting satellites. But, since no detector is sensitive to all wavelengths of the stellar spectrum, to obtain the bolometric magnitude from any other magnitudes, some corrections need to be applied. In particular, the difference between the photo visual and bolometric magnitude magnitudes of a star is called the bolometric correction, in short BC. Mathematically,
BC = mbol - mpv = Mbol - Mpv [Don’t be confused by ealier notation mvis with mpv , both are technically same].
As previous, absolute bolometric magnitude (abm) is the bolometric magnitude the star would have if it was placed at a distance of 10 parsecs from Earth.
The corrections required to reduce visual magnitudes to bolometric magnitudes are large for very cool stars and for very hot ones, but they are relatively small for stars such as the Sun.
Photo visual magnitude:
The magnitude of a celestial body that is determined by observations with a photographic plate and filter combination giving nearly the same yellow-green sensitivity as the human eye and that is nearly equal to the visual magnitude.
Radiometric Magnitude:
As the photoelectric cells and photographic plates are insensitive to infra-red radiation mainly from the cool stars, thermocouples are used for the measurement of such radiation. The corresponding magnitude is called the radiometric magnitudes. Photoconductive cells and bolometric can also be used in this region.
