Image © Joseph W. Paulini / Argonne National Laboratory.
Superconductivity is the phenomenon of a material where the electrical resistance vanishes (whereby a charge moves through a material without resistance) and the magnetic flux fields are expelled from the material. Such materials are called superconductors. It was first observed in 1911 by the Dutch physicist Heike Kamerlingh Onnes and his team while they were studying the properties of matter at very low temperature. While they were working, they discovered that the electrical resistance of mercury goes to zero below 4.2 K (-269°C). Later research revealed that the majority of chemical elements become superconducting at sufficiently low temperature.
Typical conductors lose some energy in the form of heat and others and decrease the efficiency required but superconductors allow the electrical energy to be transferred between two points with perfect efficiency, losing nothing to heat.
Though beneficial, creating superconductor is not an easy task, especially at room temperature. Recently in 2020, a team of researchers identified a novel approach to room temperature superconductivity problem.
But why is it a challenge to get room temperature superconductivity ?
A room-temperature superconductor is a material that is capable of exhibiting superconductivity at operating temperatures i.e. above 0 °C (273 K; 32 °F) - temperatures that can be reached and easily maintained in an everyday environment.
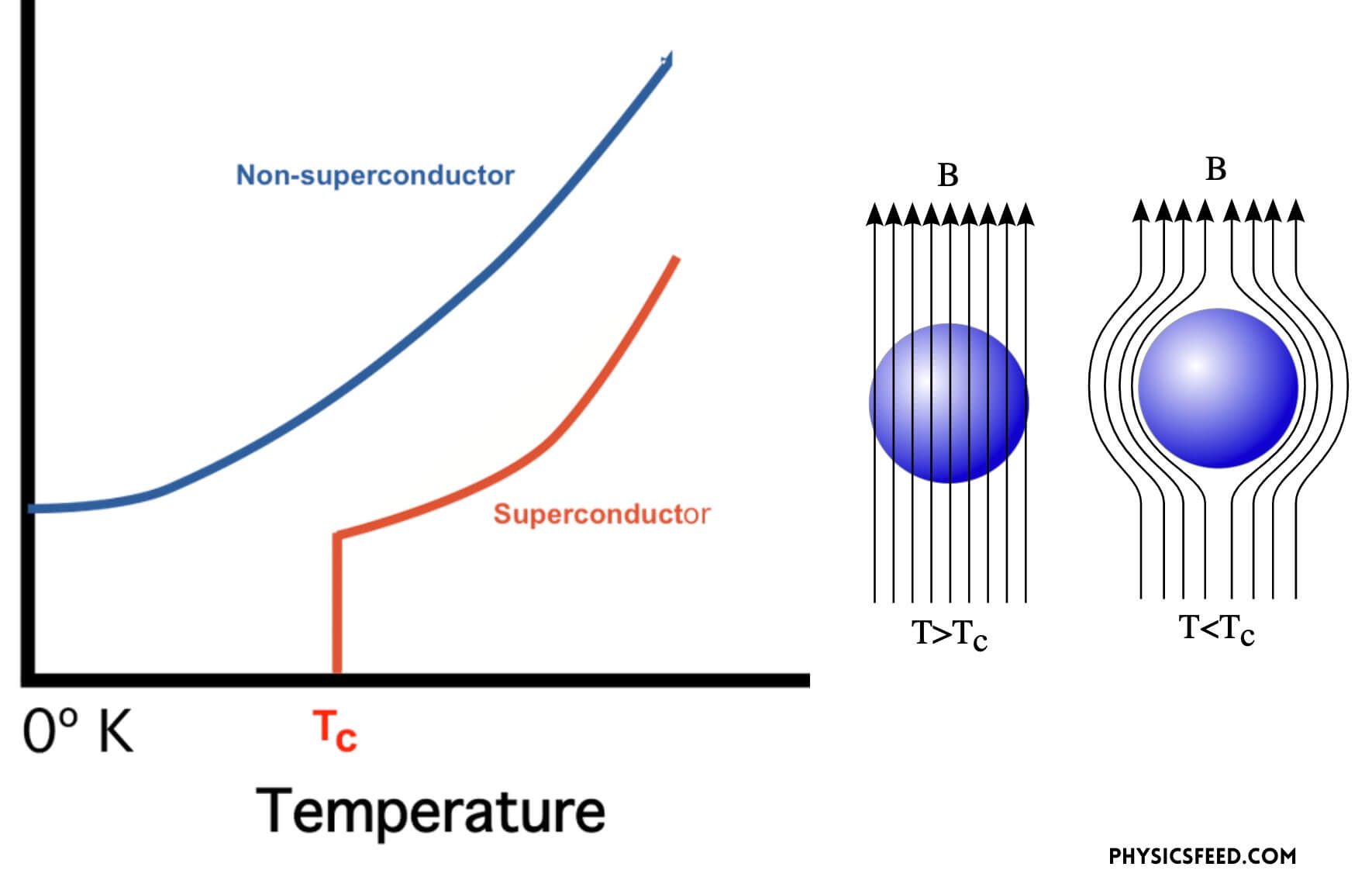
The phenomenon of normal material undergoing to superconducting phase happens when the material is driven below a temperature point called the critical temperature (TC) at which the electron almost freeze. Once the material goes below TC, the material is characterized by two basic properties: firstly, they offer no resistance to the passage of electrical current. When resistance falls to zero, a current can circulate inside the material without any dissipation of energy. Secondly, provided they are sufficiently weak, external magnetic fields will not penetrate the superconductor but remain at its surface. This field expulsion phenomenon is known as the Meissner effect, after the physicist who first observed it in 1933.
Several research like 1, 2, and 3 were already published where they achieved superconductivity above 203 K, 250 K, and 260 K respectively but with certain constrained conditions. So the processes are limited and not enough for everyday use.
But in reality, obtaining the room temperature superconductivity is affected by many aspects.
Superconductivity is based on two electrons transport phenomenon, called a Cooper pair, coordinating in such a way as to lower their overall energy in a solid.
First here is the theoretical reason behind this overdue discovery of the room temperature of superconductivity.
It was only in 1957 that three American researchers - John Bardeen, Leon Cooper and John Schrieffer - established the microscopic theory of superconductivity. According to their “BCS” theory, electrons group into pairs through interaction with vibrations of the lattice (so-called “phonons”), thus forming “Cooper pairs” which move around inside the solid without friction. The solid can be seen as a lattice of positive ions immersed in a cloud of electrons. As an electron passes through this lattice, the ions move slightly, attracted by the electron’s negative charge. This movement generates an electrically positive area which, in turn, attracts another electron. The energy of the electron interaction is quite weak and the pairs can be easily broken up by thermal energy – this is why superconductivity usually occurs at very low temperature. However, the BCS theory offers no explanation for the existence of “high-temperature” superconductors around 80 K (-193°C) and above, for which other electron coupling mechanisms must be invoked.
The physical phenomenon arises from attractive interaction between the electrons in the metal, induced by their coupling of lattice vibrations. The attractive forces create a bosonic bound state called the Cooper pair, and the transition is caused by the Bose-Einstein condensation of these bosons.
When the Cooper pair exists in this state there is an energy gap between this state of the two electrons in coordination and the state in which the two electrons are separated called the superconducting energy gap. The superconducting energy gap is very small for most solids; typically in the range of only a few millielectron volts (meV).
The energy available from the surroundings that any particle can absorb is called the thermal energy which is in practise roughly kBT, kB being Boltzmann’s constant and T the temperature.
At room temperature, this (kBT) amounts to 25 meV which is plenty of energy to break up a Cooper pair while at cryogenic temperatures like 10 kelvin, kBT is only about 1 meV. Now in this type of surrounding where very little thermal energy is available, the Cooper pair is what we called “protected”. It will only rarely absorb the energy required to jump out of the coordinated superconducting state and end up as two separate, ordinary electrons. As long as there are enough Cooper pairs in the solid they will just short out any conduction by the ordinary electrons. Both Cooper pairs and ordinary electrons exist in a superconducting metal.
As the temperature increases, the value of kBT also increases and so the thermal energy increases. Remember that thermal energy is the energy of the surrounding electron and becomes unstable. Now the those “protected” Cooper pairs become “unprotected” and the Cooper pair ultimately is no longer a Cooper pair hence breaking the superconductivity.
Though the direct method is hard researchers are twisting the methods they can get the superconductivity at room temperatures and high-temperature superconductivity. For instance, in recent research published in the journal Nature researcher obtained superconductivity in a carbonaceous sulfur hydride system at a maximum superconducting transition temperature of 15 °C (59 °F) at a pressure of 267 gigapascals (GPa).
